Electric Scenarios

An electric scenario describes the operation of an electric network according to conditions specified in the scenario properties and events. An electric scenario can determine network operational parameters such as power flow quantities, nodal voltages, generation dispatch, and shadow prices across the network, to name a few. The conditions at which these variables are evaluated are specified by the events of the electric scenario, or adopted by default values specified at the network level. The properties and settings of an electric scenario define aspects such as the time span, resolution, and numerical tolerances adopted for the solution while the mathematical equations being respected are relevant to the type of scenario applied.

There are two broad categories of electric scenarios: steady state, and quasi-dynamic, where the distinguishing factor is a steady state looks at a single timestep, and the latter multiple timesteps. Additional distinctions, such as optimality, the linear approximation notated as DC, or the unit commitment application, further characterize these two broad categories. The direct current unit commitment optimal power flow scenario (DCUCOPF) and the capacity expansion model scenario (CEM) are treated independently in this documentation, due to the additional optimization criteria that characterizes these scenarios.

1. Steady scenarios

The steady scenario represents the system at a single time instance in a power flow equilibrium condition. It can be used to analyze the operation of an electric network at a particular dispatch, to assess the voltage magnitudes and angles. Table 1 provides an overview of the five different types of steady scenarios available in SAInt.

Table 1. Steady electric scenario types.
Scenario type	Description
`SteadyUACPF`	Steady unbalanced alternating current power flow. Simulation of unbalanced power flow in an electric network subject to the AC power flow equations.
`SteadyACPF`	Steady alternating current power flow. Simulation of balanced three-phase power flow in an electric network subject to the AC power flow equations.
`SteadyACOPF`	Steady alternating current optimal power flow. Optimization of electricity generation dispatch in a balanced electric network considering transmission constraints subject to the AC power flow equations.
`SteadyDCPF`	Steady direct current power flow. Simulation of power flow in an electric network using a linear approximation (DC) for AC power flow equations.
`SteadyDCOPF`	Steady direct current optimal power flow. Optimization of electricity generation dispatch in an electric network considering transmission constraints using a linear approximation (DC)for AC power flow equations.

1.1. Scenario settings

The properties of a steady scenario allow the user to specify solver settings, time-related information, general attributes, and chart visualization options when accessed using the property editor. Solver settings provide control over the residual tolerances and the maximum number of iterations admitted during the numerical solution of the electric power flow problem. The time settings associated with a steady scenario are simply the time of the single instance, although the properties as related to quasi-dynamic scenarios will still be visible to the user. Table 2 provides an overview of the solver properties for a steady scenario, while Table 3 shows the time-related properties.

Table 2. Solver settings of a steady scenario.
Display Name	Description
`ResidualTolerance`	Residual tolerance applied to conclude on success of the solution method.
`MaxIterationSteps`	Maximum number of iteration steps for the solution method.
`UseIVModel`	Use the current-voltage formulation for ACPF and ACOPF scenarios. The default is to have the option not selected. The option is only available for AC power flow scenarios (UACPF, ACPF, ACOPF, and the related quasi-dynamic types).

Table 3. Time settings of a steady scenario.
Display name	Description
`StartTime`	This is the time of the single instance that is executed with the steady scenario.
`EndTime`	This property is not relevant to the steady scenario, but it will always be visible and show a value one hour later than the `StartTime`.
`TimeWindow`	The steady scenario has no length of time because it represents a single instance in time. However, this value will still show the difference between `EndTime` and `StartTime`, which will be a fixed one-hour duration due to the automatic setting of the `EndTime` property.
`TimeStep`	The `TimeStep` property is not relevant to the steady scenario, but it will be visible and show the default value of 60 minutes.
`StepsTimeWindow`	The `StepsTimeWindow` property is not relevant to the steady scenario, but it will be visible and show a default value of 1.
`IniState`	Name of the scenario whose terminal state is used as the initial state for the current scenario. Default is set to none. This is an optional property, and not relevant for a steady scenario.

2. Quasi-dynamic scenarios

Quasi-dynamic electric scenarios (AC and DC) comprise power flow (PF) and optimal power flow (OPF) simulations. A succession of steady scenarios comprises a quasi-dynamic scenario. Quasi-dynamic AC/DC PF scenarios are a succession of independent steady simulations, while quasi-dynamic AC/DC OPF scenarios are a succession of optimizations where generator constraints are considered between consecutive timesteps. Table 4 provides an overview of the four different types of quasi-dynamic scenarios available in SAInt.

Table 4. Quasi dynamic electric scenario types.
Scenario type	Description
`QuasiDynamicUACPF`	Quasi-dynamic unbalanced alternating current power flow A succession of independent simulations of unbalanced power flow in an electric network subject to the AC power flow equations.
`QuasiDynamicACPF`	Quasi-dynamic alternating current power flow A succession of independent simulations of balanced three-phase power flow in an electric network subject to the AC power flow equations.
`QuasiDynamicACOPF`	Quasi-dynamic alternating current optimal power flow. A succession of optimizations of electricity generation dispatch in an electric network considering transmission constraints subject to the AC power flow equations. Generator ramping constraints are taken into account between consecutive timesteps.
`QuasiDynamicDCPF`	Quasi-dynamic direct current power flow. A succession of independent simulations of power flows in an electric network using a linear approximation (DC) of the AC power flow equations.
`QuasiDynamicDCOPF`	Quasi-dynamic direct current optimal power flow. A succession of optimizations of electricity generation dispatch in an electric network considering transmission constraints using a linear approximation (DC) of the AC power flow equations. Generator ramping constraints are considered between consecutive timesteps.

2.1. Scenario settings

The properties of a quasi-dynamic scenario allow the user to specify solver settings, time-related information, general attributes, and chart visualization options when accessed using the property editor. Solver settings provide control over the residual tolerances and the maximum number of iterations admitted during the numerical solution of the quasi-dynamic electric problem formulation. Voltage formulation settings can be optionally selected. The time settings for a quasi-dynamic scenario define the optimization time window, the start time and the end time, the time step, and an optional scenario providing the initial conditions, constituting the operational snapshot of the system prior to the beginning of the scenario. Table 5 provides an overview of the solver’s properties for a quasi-dynamic scenario, while Table 6 shows the time-related properties.

Table 5. Solver settings of a quasi-dynamic electric scenario.
Display name	Description
`ResidualTolerance`	The residual tolerance for linearization steps.
`MaxIterationSteps`	The maximum number of iteration steps for the problem linearization.
`UseIVModel`	Use the current-voltage formulation for ACPF and ACOPF scenarios. The default is to have the option not selected. The option is only available for AC power flow scenarios (UACPF, ACPF, ACOPF, and the related quasi-dynamic types).

Table 6. Time settings of a quasi-dynamic electric scenario.
Display name	Description
`StartTime`	The start time of the scenario. This is the first time step in a scenario. The default is to set the calendar day and hour of when the scenario is created by the user.
`EndTime`	The end time of the scenario. This is the final time step in a scenario. The default is to set the hour and a plus one calendar day of when the scenario is created.
`TimeWindow`	The total simulation time window or the total amount of time in a scenario (i.e., the difference between `EndTime` and `StartTime`).
`TimeStep`	A time step is a fraction of the scenario time window used for discretizing the scenario time window into distinct time points which are calculated for the variables. The time window is a multiple of the time step, i.e. `TimeWindow` divided by `TimeStep` must be an integer greater than or equal to one. The default is to have a 900 second (i.e., 15 minutes) timestep.
`StepsTimeWindow`	The number of time steps for the scenario time window (i.e. `TimeWindow` divided by `TimeStep`).
`IniState`	Name of the scenario whose terminal state is used as the initial state for the current scenario. This is an optional property, and the default is set to none. The property is in the "General" section of the property editor.

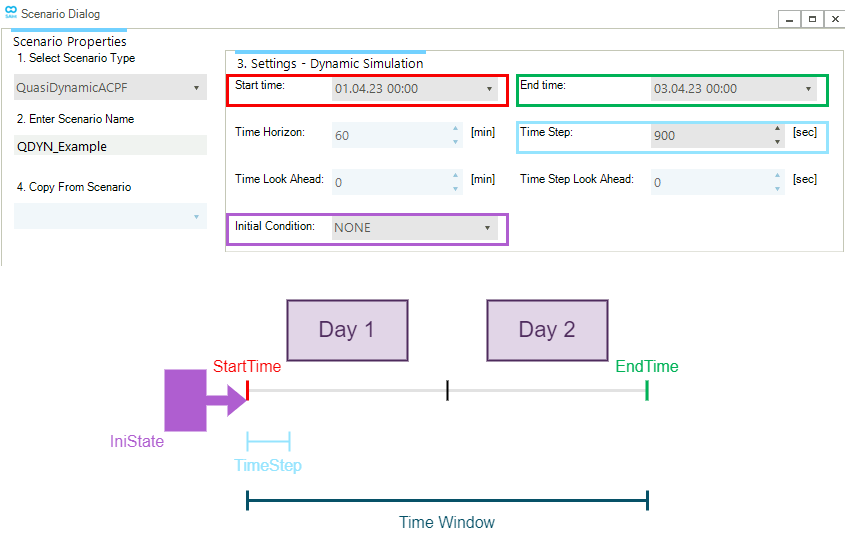
Figure 1 shows an example of the time settings and the associated graphical description of a quasi-dynamic ACPF scenario as available in the Scenario Dialog window.

Figure 1. Example of times settings and graphical description of a quasi-dynamicACPF scenario.

3. DCUCOPF scenarios

The DCUCOPF is a scenario for optimizing decisions on unit commitment and economic dispatch considering transmission constraints. It analyzes the operation of an electric network under time-varying boundary conditions (e.g., TimeWindow, TimeLookAhead, etc.). The optimization can be multi-time step, and each optimization window can have a look ahead period to inform decisions that influence the state of the network beyond the end of the optimization window.

3.1. Scenario settings

The properties of a DCUCOPF scenario allow the user to specify solver and time-related information, as well as general attributes and chart visualization options. Solver settings provide control over the solver type, the solver model, the time limit, and the relative MIP gap. Optionally, the user can write to an external file the linear programming problem for the optimization of the active model. The time settings for a DCUCOPF scenario define, as for a quasi-dynamic scenario, the optimization time window, the start time and the end time, the time step for the time horizon, and an optional scenario providing the initial conditions, constituting the operational snapshot of the system prior to the beginning of the scenario. Furthermore, the user can specify the time look ahead, the time step look ahead, and the time horizon. Table 7 provides an overview of the solver’s properties for a quasi-dynamic scenario, while Table 8 shows the time-related properties.

Table 7. Solver settings of a DCUCOPF scenario.
Display name	Description
`SolverType`	Solver type to use for solving the LP and MIP. The available option is Gurobi. Other options may be available in future releases.
`SolverModel`	The type of solver model to use. Choices are: MIP and LP. Default is MIP.
`SolverTimeLimit`	The time limit for the DCUCOPF solver. If the relative mip gap is not achieved within the solver time limit, the latest solution found is considered as the result of the time horizon. Default is 3600 seconds.
`RelativeMipGap`	The relative mip gap for branch and bound algorithm (i.e., relative difference between best integer objective and the best objective in the remaining unbranched nodes in the branch and bound tree). Default is 1.0E-3.
`WriteLPFile`	Indicates if an LP file of the optimization model should be generated. This file lists the objective functions and all the linearized equations. Default is to not generate the file.

Table 8. Time settings of a DCUCOPF scenario.
Display name	Description
`StartTime`	Start time of the scenario. It is the first time step in a scenario. The default is to set the calendar day and hour of when the scenario is created.
`EndTime`	End time of the scenario. It is the final time step in a scenario. The default is to set the hour and a plus one calendar day of when the scenario is created.
`TimeWindow`	The total amount of time in a scenario (i.e. the difference between `EndTime` and `StartTime`).
`TimeHorizon`	The time horizon is a fraction of the scenario time window considered for a consecutive optimization in a DCUCOPF scenario. The time window is a multiple of the time horizon, i.e. `TimeWindow` divided by `TimeHorizon` must be an integer greater than or equal to one. This integer represents the number of consecutive optimizations for a DCUCOPF scenario. Each consecutive optimization covers a time interval of the scenario time window equal to the time horizon. Default is set to 60 minutes.
`TimeStep`	A time step is a fraction of the scenario time window used for discretizing the scenario time window into distinct time points which are calculated for the variables. The time window is a multiple of the time step, i.e., `TimeWindow` divided by `TimeStep` must be an integer greater than or equal to one. Default is set to 900 seconds (i.e., 15 minutes). In DCUCOPF, SAInt uses the label "Time Step Horizon" to better clarify the concept.
`TimeLookAhead`	A look ahead, look ahead time, or time look ahead is a time duration added to the time interval considered in the consecutive optimization for a DCUCOPF scenario. It assists the mathematical model in finding a more realistic solution for the commitments of generators and the operation of storages close to the end of a time horizon as it indicates that the operation of the generators does not end at the end of the time horizon. The total time interval for a consecutive optimization is composed of the `TimeHorizon` and the `TimeLookAhead`. Default is set to zero minutes.
`TimeStepLookAhead`	The time step for the look ahead. It typically has a smaller time resolution or a longer time step than the time horizon. Default is set to zero seconds.
`IniState`	Name of the scenario whose terminal state is used as the initial state for the current scenario. Default is set to none. This is an optional property.
`ConsecutiveRuns`	Number of consecutive runs for a given time horizon and scenario time window (i.e., `TimeWindow` divided by `TimeHorizon`). This is a derived option.
`StepsTimeWindow`	The number of timesteps for the scenario time window (i.e., `TimeWindow` divided by `TimeStep`). This is a derived option.
`StepsTimeHorizon`	The number of time steps per time horizon (i.e., `TimeHorizon` divided by `TimeStep`). This is a derived option.
`StepsLookAhead`	The number of time steps per look ahead (i.e., `TimeLookAhead` divided by `StepsLookAhead`). This is a derived option.
`IniState`	Name of the scenario whose terminal state is used as initial state for the current scenario. Default is set to none. This is an optional property.

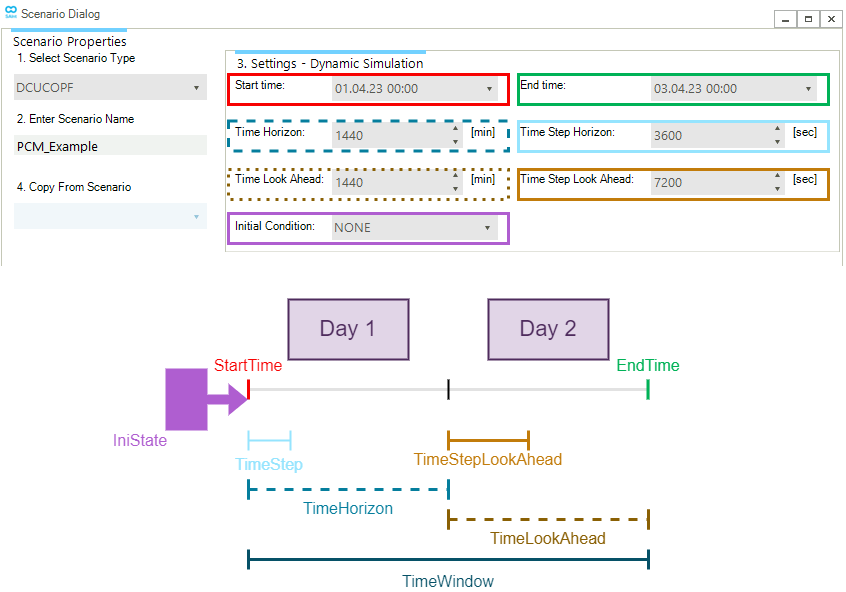
Figure 2 shows an example of the time settings and their graphical description of a DCUCOPF scenario available in the Scenario Dialog.

Figure 2. Example of times settings and graphical description of a DCUCOPF scenario.

By default, the event NOLASTHOR is set to False. If the sum of the TimeHorizon and TimeLookAhead of the last consecutive run exceeds the EndTime, the fraction of the TimeLookAhead that extends beyond the EndTime is truncated. For example, with a TimeWindow of 6 days, 2 days TimeHorizon, and 3 days TimeLookAhead, SAInt will execute 3 consecutive runs, where in the first run, the last TimeLookAhead is of 3 days, in the second run of 2 days, and in the last run is completely truncated rather than being of 2 days. In this example, if the event NOLASTHOR is set to True (not recommended), the last TimeLookAhead is completely neglected.

4. CEM scenarios

The CEM is a scenario for identifying the least-cost mix of power system resources, considering future scenarios like new policies, technologies, demand forecasts, and fuel price projections.

4.1. Scenario settings

The properties of a CEM scenario allow the user to specify solver, solution algorithm, and time-related information. The time settings for a CEM scenario define the list of investment years, the time step for the operational model, and parameters related to the time series input data like demand forecast and renewable availability. Table 9 provides an overview of the solver-related properties, while Table 10 shows the time-related properties. These properties are specified in two input files, namely ScenarioInfo.csv and HorizonInput.csv.

Table 9. Solver settings of a CEM scenario.
Display name	Description
`doStepInterpolation`	If true (=1), every investment year represents all years (including itself) until the next investment year. The last year in the horizon only represents itself. It is recommended to enable this parameter.
`useAnnuityMethod`	If true (=1), uses the annuity method to annualize investments while considering discount rates (same nominal value every year). If false (=0), the investment is split equally over the lifetime (same NPV every year).
`DecimalResolution`	Decimal resolution of the output values.
`doOverwriteOutput`	If true (=1), the 'Output' folder is deleted before the model run.
`doCompactTimeseries`	If true (=1), prints out the time series data in the form of representative periods.
`doExpandedTimeseries`	If true (=1), prints out the time series data (including repetitive days) in the form of an expanded yearly time series.
`writeSolverLog`	If true (=1) the log from the optimization solver will be printed to the console during the solution process.
`writeLP`	If true (=1) an LP file of the optimization model will be generated. This file lists the objective functions and all the linearized equations. Default is to not generate the file.
`LPMethod`	Controls the algorithm used by Gurobi to solve the optimization. Set this parameter to 1 to choose Dual Simplex, which might improve performance in large models. The default value is -1 which makes an automatic choice of the algorithm.

Table 10. Time settings of a CEM scenario.
Display name	Description
`horizon`	The unique ID of the optimization horizon. Currently only allowed to have a single horizon with ID = 1.
`year`	The year for which investment decisions will be made. Additional years for multi-stage problems can be listed in different rows.
`deltaT`	The size of the operational time step (in hours) for the year being modeled.
`RepPeriodLength`	Length of one representative period (in hours).
`TimestepsPerPeriod`	Number of timesteps in the input data per period (a positive integer value).